KDS transformation to improve compression ration
KDS - transformation stands for Keep Dominant Symbols - transformation. The advantage of this method is that those statistical properties of the input stream that can be efficiently used by any compression algorithm are not dramatically changed.
Consider the following procedure to build a Huffman code for an alphabet V, where pa is the probability of appearance of symbol a in an input source:
- if |V|=2 then V={a,b} and code(a)=0 and code(b)=1.
- if |V|>2 then select from V two symbols with
smallest probabilities (call them a and b).
Then code(a)=code(#)0, code(b)=code(#)1,
where # is a new symbol with p# = pa + pb,
and
code(#) is computed applying the same procedure with the alphabet
V \ {a,b}
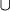 {#}.
{#}.
The same is the essence of this transformation, to replace symbols with low probabilities with a new symbol.
Further we present formally this transformation.
Consider A is an alphabet and w is a word over the alphabet A. Consider A = R
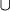 D with
|R| = |D|, where R is a subset
of the alphabet A containing the "rare" symbols and D a subset
containing the "dominant" symbols in the word w.
D with
|R| = |D|, where R is a subset
of the alphabet A containing the "rare" symbols and D a subset
containing the "dominant" symbols in the word w.
Is is easy to see that there is an unique decomposition of w:
where:
- ri
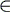 R+, 1 < i
R+, 1 < i 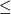 k ;
k ;
- r1
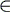 R*;
R*;
- di
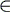 D+, 1
D+, 1 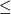 i < k ;
i < k ;
- dk
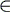 D*.
D*.
The first step of our transformation is rewriting w in w', where:
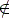 A.
A.
Consider now a bijective mapping: f:R
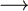 D.
In the second
step of the transformation the string w'' is obtained in the
following way:
D.
In the second
step of the transformation the string w'' is obtained in the
following way:
In the final step the new symbol # and an explicit representation of the mapping f are added at the beginning of string w''. This way the string w''' is obtained:
The reverse transformation works in the following way: given a string w'''(obtained as above) consider the first symbol of w''', as the separator #. Consider now the following factorization of w''':
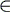 { R D }|R|,
w2
{ R D }|R|,
w2 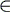 R,
w3
R,
w3 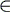 D
D 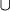 { # }.
It is easy to observe that there is an unique such a factorization of w'''.
{ # }.
It is easy to observe that there is an unique such a factorization of w'''.
A Case Study
We present here the effect of this transformation combined with some traditional compression methods.The length (in bits) of the Lempel-Ziv code of a word w
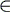 V* is:
V* is:
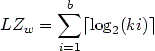
Consider now the case of the alphabet A where |A|=2p, p > 1. Let u and v be two words, u
 A* and
v
A* and
v  (A
(A  { # } )*
, v is obtained form u using the above
transformation.
{ # } )*
, v is obtained form u using the above
transformation.
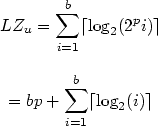
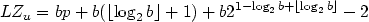
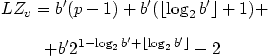
If
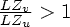 compression is improved by
transformation presented above.
compression is improved by
transformation presented above.
An implementation of this algorithms improve compression from 5\% up to 10\% in combination with compression tools like gzip. In the following table some experimental results are presented:
| Original size | gzip | KDS+gzip |
| 104448 | 19926 | 19756 |
| 263680 | 68084 | 68527 |
| 829440 | 211659 | 202124 |
| 913755 | 293157 | 287293 |
| 1691136 | 424372 | 407384 |
| 2156032 | 511538 | 489263 |
| 3259904 | 597233 | 579094 |
| 5751296 | 1321138 | 1278913 |
| 6125056 | 1168909 | 1126271 |
| 28844032 | 6409980 | 6228254 |
Download:KDS transformation implementation in Visual C++.
