2.1.1.2 Arithmetic Codes

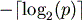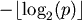Huffman codes rarely produces best results (only when probabilities of occurrence of the symbols are negative powers of 2), because the length of a code assigned to a symbol with the probability of occurrence p is or Arithmetic coding, developed by J. J. Rissanen and G. G. Langdon in 1979, overcome this problem. In theory, arithmetic codes assign one "codeword" to each possible input sources. The codewords consist of half-open subintervals of the half-open unit interval [0,1), and are expressed by specifying enough bits to distinguish the subinterval corresponding to the actual input source from all other possible subintervals.

As in Section Huffman Codes, consider V an alphabet, and s V⁺ an input source. For any symbol a V consider p_a the probability of occurrence of this symbol in the input source. We can consider the alphabet V of size k as the set of integers {0,1,2,...,k-1}. We present further the method to construct the intervals associated to all prefixes of the input source s.

• the code associated to 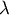is [0,1);
• if u and u j, where j 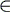V, are both prefixes in s and the code associated to u is [a,b), then the code associated to u j is [a_j,b_j) where:
  
  
  

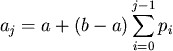
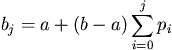
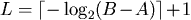Consider I(s)=[A,B) is the subinterval associated to the entire input source using the procedure above. Let . The number consist of the first L bits of the binary expansion, let say B(s), of the midpoint of I(s) uniquely identified this interval and this is the final code.
As in the case of Huffman encoding, arithmetic decoder should know the statistical model used by the encoder. So the decoder knows the probability p_a of any symbol a from the alphabet V={0,1,...,k-1}. Decoder works in the opposite way. It starts reading the binary sequence B(s) and consider the rational number r=.B(s). Starts with an initial interval [0,1) and proceed in the following way:

• if the current interval is [a,b) compute:   
  a₀ = a;   
  
  b₀ = a + ( b - a ) p₀;     
  ...   
  
  a_j = a + ( b - a )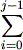 p_i;   
  
  b_j = a + ( b - a )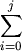 p_i;     
  ...   
  a_k = a + ( b - a )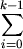 p_i;   
  
  b_k = a + ( b - a )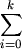 p_i;
  and found x such that r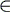 [a_x,b_x). Decoder outputs x, current interval became [a_x,b_x) and repeat the procedure.

Remark 1. The decoding procedure above does not have a stop criterion. Encoder should provide some mechanism to indicate the end of the input source, either a special character added to the end of the input source coded just once, or some indication of the inputs's length.