

2.1.1.1 Huffman codesA brief introduction to codes theoryA code over an alphabet U is any set C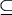 U+
satisfying U+
satisfying
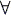 u1,...,um,v1,...,vn
u1,...,um,v1,...,vn
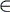 C )
( u1...um = v1...vn C )
( u1...um = v1...vn
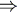 u1 = v1 ) u1 = v1 )
An encoding of an input source s 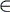 V+ is a bijective
mapping: V+ is a bijective
mapping:
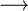 C. C.
Consider an alphabet an alphabet U and C 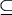 U+.
C is called
a prefix set if for any word c U+.
C is called
a prefix set if for any word c 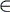 Cthere is no word
c' Cthere is no word
c' 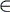 such that c is a prefix of c'. such that c is a prefix of c'.
Remark 1. Consider U is an alphabet and C 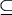 U+.
If C is a prefix set then C is a code. U+.
If C is a prefix set then C is a code.
Indeed, suppose by contradiction that C is a prefix set but is not a code. Then: 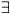 u1,...,um,v1,...,vn u1,...,um,v1,...,vn
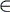 C )
(
u1...um = v1...vn
C )
(
u1...um = v1...vn
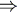 u1 != v1)
u1 != v1)
Prefix codes are also called instantaneous codes. Any instantaneous codes C 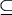 U+
satisfies Kraft
inequality: U+
satisfies Kraft
inequality:
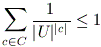
The average code-length of C with respect to the probabilities distributions of symbols form V in the input source s is: 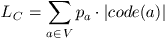
Shannons's fundamental noiseless source coding theorem says that entropy defines a lower limit of the average number of bits needed to encode the source symbols. In other word considering any encoding of an input source the average code-length is greater then entropy. Huffman codesHuffman compression technique is probably one of the most famous compression method. Since its development, in 1952, this method has been the subject of intensive research in data compression theory, being used as a stand-alone method or combined with other techniques.This is a statistical method that uses variable-size codes, assigning shorter codes to symbols or groups of symbols that appear more often in the input source. There are two main problems using variable-size codes:
The second problem (minimizing the average size of the code) is more difficult. Consider V an alphabet, and s 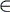 V+
an input source. For any symbol a V+
an input source. For any symbol a 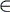 V consider pa the probability of occurrence of this symbol in the
input source. Then
V consider pa the probability of occurrence of this symbol in the
input source. Then
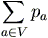 =1. =1.
Without loss of generality we may assume that for any symbol a 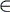 V, pa > 0.
Let U={0,1} be a binary alphabet, and let
C V, pa > 0.
Let U={0,1} be a binary alphabet, and let
C 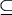 U+ be a code
(prefix set), and consider the mapping: U+ be a code
(prefix set), and consider the mapping:
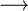 C. C.
The following restrictions will be imposed to this mapping [1]
This recursive procedure suggest the construction of a tree (actually, any prefix code can be represented as a tree). The following example will explain better the construction of a Huffman code using a tree (called Huffman tree). The labels of nodes consist of pairs (symbol, probability). Each edge descending form a node is either 0 or 1. This tree is traversed to determinate the codes of the symbols. In order to obtain the original word s from the word B(s), decoder should know the statistical model of the encoder (the probabilities of the symbols in the input source). Using those probabilities, the decoder can also build the same Huffman tree. It starts reading the word B(s) bit by bit. The Huffman tree is traversed starting from the root, according to the current bit from B(s). If a leaf is reached, decoder outputs the symbol corresponding to that leaf and return to the root of the Huffman tree. This process is repeated until all bits in B(s) are processed. Remark 2. A Huffman code is not unique, relative to a distribution probabilities of symbols in an input source. Theorem 1.Consider s 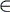 V*
an input source and
C V*
an input source and
C 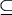 {0,1}+
a Huffman code as above.
Then, for all prefix codes C', {0,1}+
a Huffman code as above.
Then, for all prefix codes C',
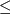 LC'. LC'.
|

|